A thing the guy told me about that he read in Murderous Maths: If you fit a right triangle into a circle with all of its corners on the circumference, the hypotenuse is always the circle's diameter. We looked up the
proof. (In the grown-up world, this is called the converse of Thales's theorem.)
The proof that was easiest for us to understand was the one that starts with a right triangle being half of a rectangle.
If you have a line going from two points along the circumference (which you do in the case of the non-hypotenuse lines of the triangle), there can be a parallel line that is also on the circumference — a mirrored line on the other half of the circle, sort of. If you draw those mirrored lines for the two non-hypotenuse lines of the triangle, you have a rectangle.
The rectangle is exactly centered within the circle. If you draw diagonal lines between opposite corners of the rectangle, you then find center of the circle where they cross. One of the diagonal lines is the hypotenuse of the original triangle. So, that hypotenuse goes through the center of the circle and is a diameter.
I have to admit, I'm still a little amazed by this basic geometry.
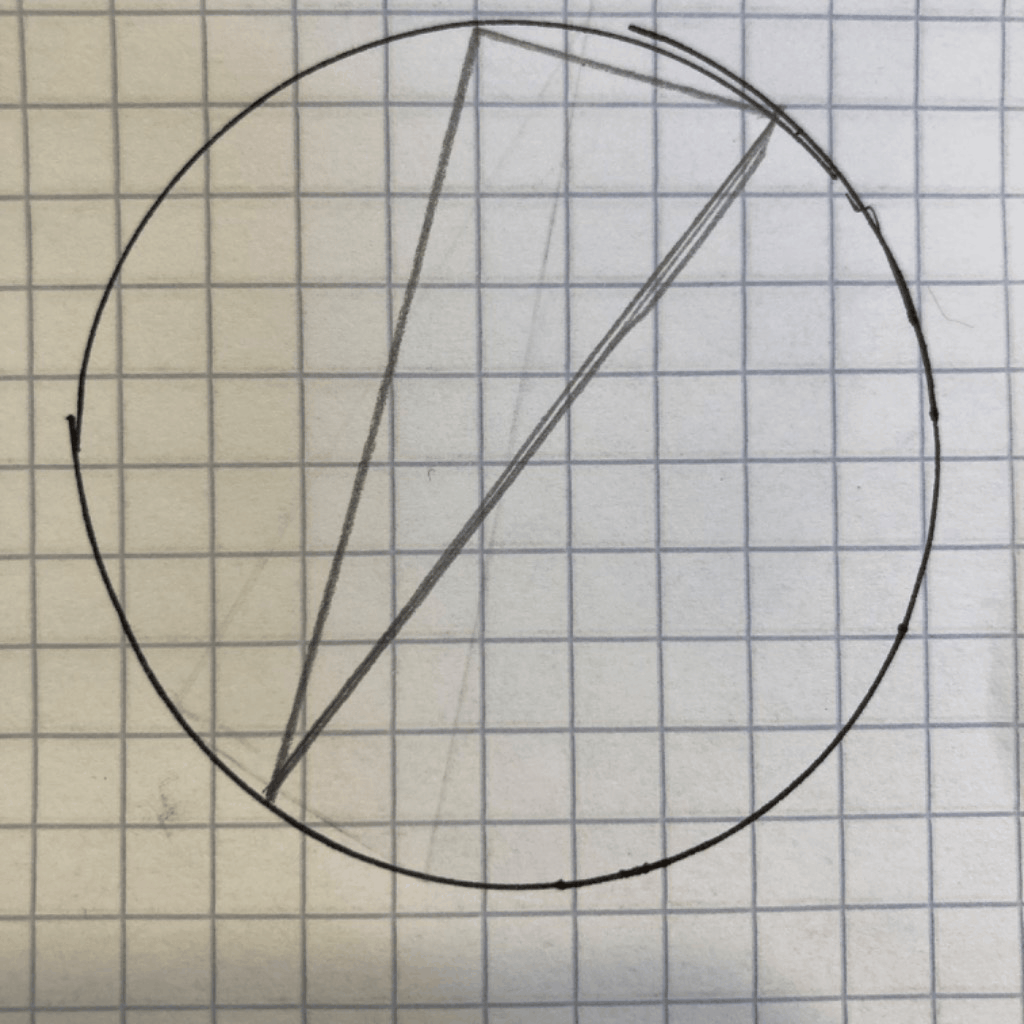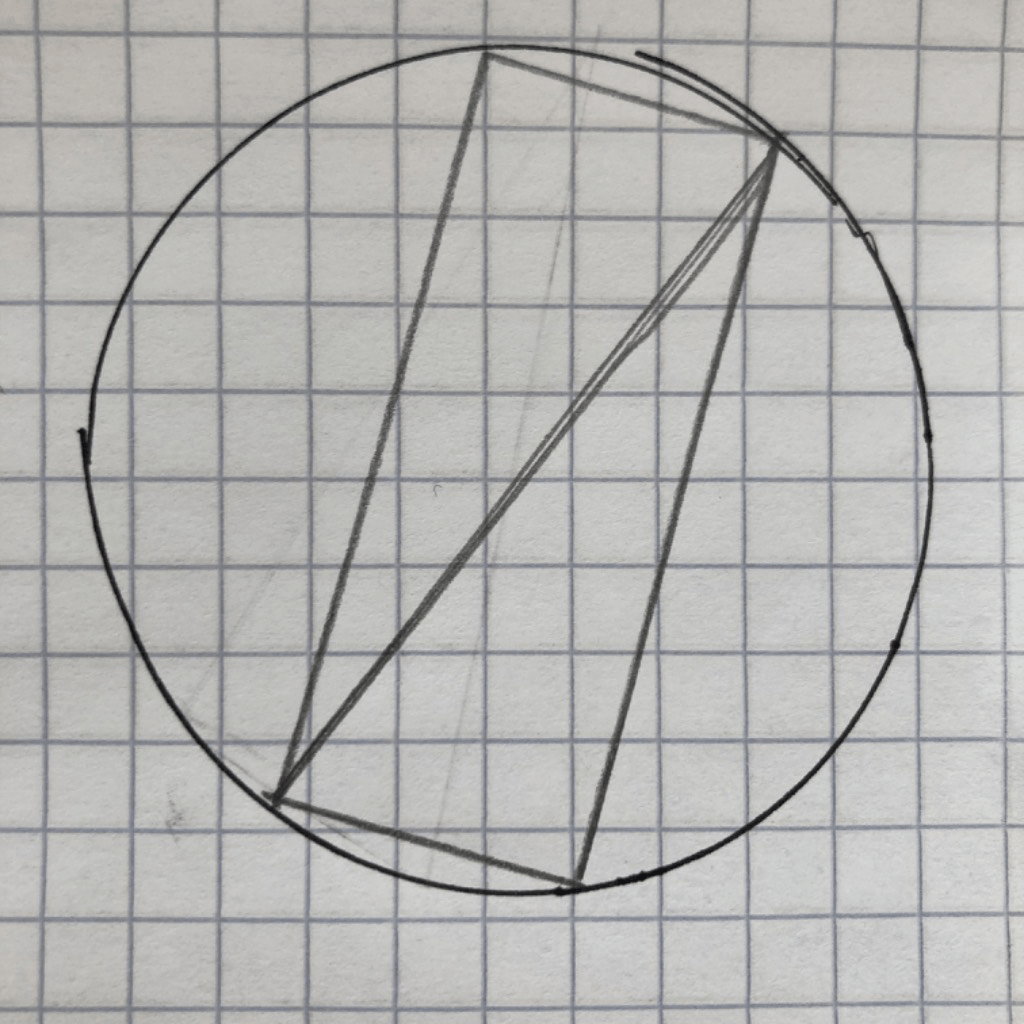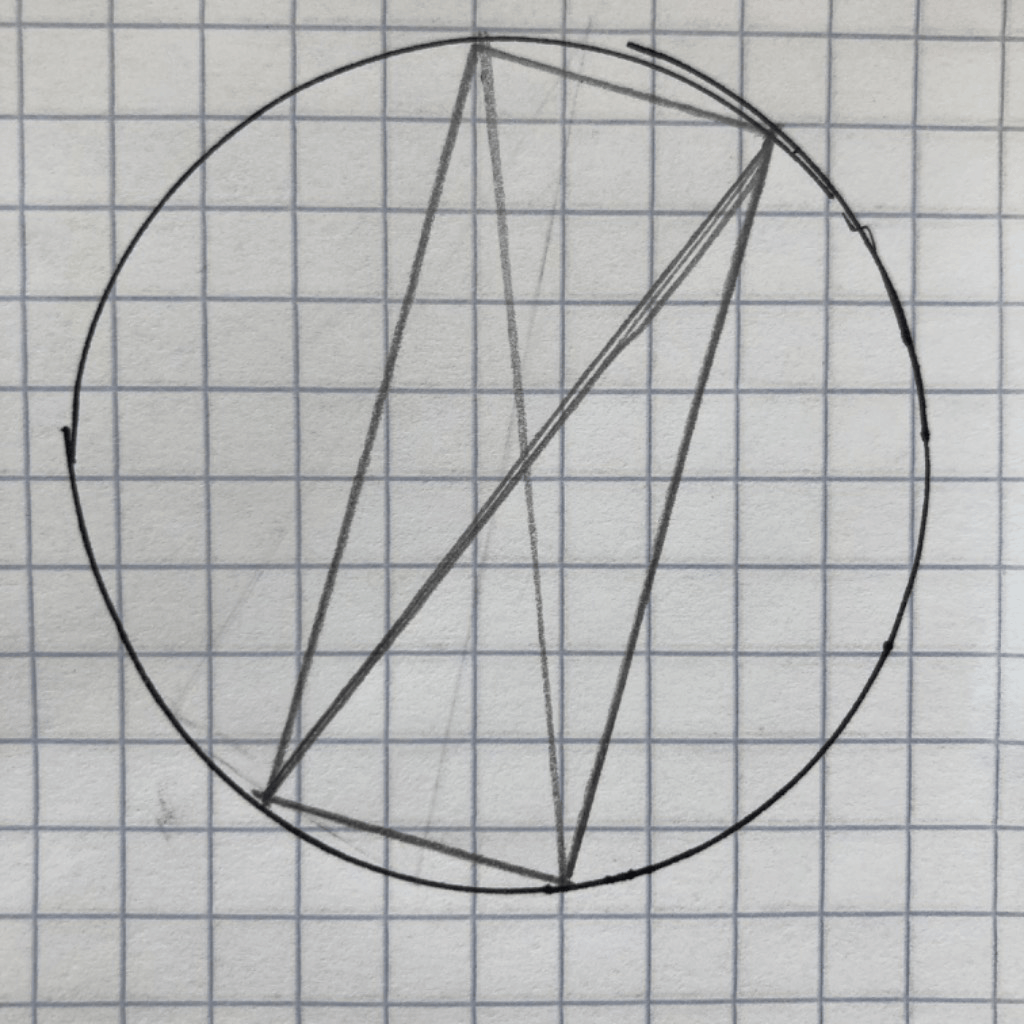A thing the guy told me about that he read in Murderous Maths: If you fit a right triangle into a circle with all of its corners on the circumference, the hypotenuse is always the circle's diameter. We looked up the proof. (In the grown-up world, this is called the converse of Thales's theorem.)